Fold Left and Right in Python
Python exposes a number of built-in functions enriched with a plethora of modules composing the Python Standard Library. It is a pragmatic language that does not confine the developer in a specific programming paradigm. A Python developer can write imperative, procedural, object oriented or functional code. In Python, common functional constructs are available as built-in functions (e.g. map, filter, all, any, sum...). Additional higher-order functions are regrouped in the functools module (e.g. reduce, partial...). Prior to crafting some Python code, let's take a detour in some potentially more arcane areas of functional programming, in particular surrounding the fold concepts.
Despite being primary a Python article, some of the initial code examples are in Haskell. Haskell is the perfect cradle for concepts like Folding. In addition, Haskell code, like Python code, reads like pseudo-code.
Fold
Fold regroups a family of higher-order functions pertaining to the functional programming domain. At a high level, folding allows to deconstruct or reduce data. A typical signature for a generic fold function is the following: $\text{fold} f\ z\ xs$
Where:
fis a higher-order function taking two arguments, an accumulator and an element of the listxs. It is applied recursively to each element ofxs.zis the initial value of the accumulator and an argument of the functionf.xsis a collection.
Fold functions come in different kinds, the two main linear ones are foldl and foldr.
foldl
foldl, for "fold left", is left associative. Think of foldl as "fold from the left":
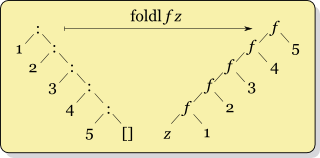
Let $\otimes$ be a variable bound to the function of two arguments f in the diagram above. The foldl function can be defined as follows:
$\text{foldl}\ (\otimes)\ z\ [1, 2, 3, 4, 5] = ((((z\ \otimes\ 1)\ \otimes\ 2)\ \otimes\ 3)\ \otimes\ 4)\ \otimes\ 5$
To cement the concept, here is an example in Haskell with the subtraction operator:
> foldl (-) 0 [1,2,3]
-6
> (((0 - 1) - 2) - 3)
-6
foldr
foldr, for "fold right", is right associative. Think of foldr as "fold from the right":
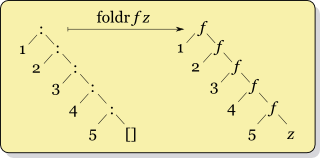
As for foldl in the previous section, let $\otimes$ be a variable bound to the function of two arguments f. The foldr operator can be defined as:
$\text{foldr}\ (\otimes)\ z\ [1, 2, 3, 4, 5] = 1\ \otimes\ (2\ \otimes\ (3\ \otimes\ (4\ \otimes\ (5\ \otimes\ z))))$
Following is an example with the division operator:
> foldr (/) 10 [1,2,3]
0.15
> 1 / (2 / (3 / 10))
0.15
Laws of fold
In the book Introduction to Functional Programming using Haskell, the authors Richard Bird and Philip Wadler wrote a section on the Laws of fold. The first three laws are called duality theorems and concern the relationship between foldl and foldr. For simplification and in the context of this article, let's focus on the first and third duality theorems.
First duality theorem
For all finite lists xs, if f is associative and has identity element e, then $\text{foldr}\ f\ e\ xs\ =\ foldl\ f\ e\ xs$
To concretely illustrate this principle in the [Haskell REPL], see the following example using the addition as operation and 0 as the identity element for addition:
> foldl (+) 0 [1,2,3]
6
> foldr (+) 0 [1,2,3]
6
> foldl (+) 0 [1,2,3] == foldr (+) 0 [1,2,3]
True
Third duality theorem
For all finite lists xs, $\text{foldr}\ f\ e\ xs\ =\ \text{foldl}\ (\text{flip}\ f)\ e\ (\text{reverse}\ xs)$
where, $\text{flip}\ f\ x\ y = f\ y\ x$
To illustrate this principle, let's take another simple example in Haskell, this time with subtraction that is not associative:
> foldl (-) 0 [1,2,3]
-6
> foldr (-) 0 [1,2,3]
2
> foldl (flip(-)) 0 (reverse [1,2,3])
2
> foldr (-) 0 [1,2,3] == foldl (flip(-)) 0 (reverse [1,2,3])
True
Fold in Python
Despite some resistance from Guido Van Rossum (see The fate of reduce() in Python 3000), Python has a Fold function. It is named reduce() and is a built-in function in Python 2. In Python 3, it can be found in the functools module: functools.reduce().
Note: The snippets of code used as examples in this article target Python 3.
foldl in Python
Python already has foldl because functools.reduce() is a foldl construct. As an exercise and to mimic Haskell, a foldl function can be written as follows with a lambda:
>>> import functools
>>> import operator
>>> foldl = lambda func, acc, xs: functools.reduce(func, xs, acc)
>>> foldl(operator.sub, 0, [1,2,3])
-6
>>> foldl(operator.add, 'L', ['1','2','3'])
'L123'
Or more formally as a function:
import functools
import operator
def foldl(func, acc, xs):
return functools.reduce(func, xs, acc)
# tests
print(foldl(operator.sub, 0, [1,2,3])) # -6
print(foldl(operator.add, 'L', ['1','2','3'])) # 'L123'
foldr in Python
Relying on the third duality theorem evoked in the Laws of fold section above, foldr can be crafted as a lambda:
>>> import functools
>>> import operator
>>> foldr = lambda func, acc, xs: functools.reduce(lambda x, y: func(y, x), xs[::-1], acc)
>>> foldr(operator.sub, 0, [1,2,3])
2
>>> foldr(operator.add, 'R', ['1', '2', '3'])
'123R'
Note:
xs[::-1]is the Python idiomatic way to return the reverse of a list (see this answer from Alex Martelli on stackoverlow). The other option, more readable, is to use the built-in reversed function.
Lambdas implemented as above are not generally conducive of good code readibilty. The following code, although longer, may be arguably more maintainable:
import functools
import operator
def flip(func):
@functools.wraps(func)
def newfunc(x, y):
return func(y, x)
return newfunc
def foldr(func, acc, xs):
return functools.reduce(flip(func), reversed(xs), acc)
# test
print(foldr(operator.sub, 0, [1,2,3])) # 2
print(foldr(operator.add, 'R', ['1','2','3'])) # '123R'
Note: the flip function above is courtesy of Raymond Hettinger in a stackoverflow answer
Now what?
We now have new toy functions in Python, foldl and foldr, what can we do with those?
Reimplementing existing functions with reduce (foldl)
The folding concept opens the doors to build many other functions. It allows to be done without having recourse to writing explicit recursive code or managing loops. For example, max, min, sum, prod, any, all, map, filter among others, can all be defined with folding/reduce functions.
Here are some simplistic examples, using lambdas for conciseness:
>>> import functools
>>> import operator
>>> lmax = lambda xs: functools.reduce(lambda x, y: x if x > y else y, xs)
>>> lmax([1,2,3,4,5])
5
>>> lmin = lambda xs: functools.reduce(lambda x, y: x if x < y else y, xs)
>>> lmin([1,2,3,4,5])
1
>>> lsum = lambda xs: functools.reduce(operator.add, xs)
>>> lsum([1,2,3,4,5])
15
>>> product = lambda xs: functools.reduce(operator.mul, xs)
>>> product([1,2,3,4,5])
120
>>> lany = lambda pred, xs: functools.reduce(lambda x, y: x or pred(y), xs, False)
>>> lany(lambda x: x > 3, [1,2])
False
>>> lany(lambda x: x > 3, [1,2,3,4,5,6])
True
>>> lall = lambda pred, xs: functools.reduce(lambda x, y: x and pred(y), xs, True)
>>> lall(lambda x: x > 3, [4,5,6,7])
True
>>> lall(lambda x: x > 3, [1,2])
False
>>> lmap = lambda func, xs: functools.reduce(lambda x, y: x + [func(y)], xs, [])
>>> lmap(lambda x: x + 2, [1,2,3,4,5])
[3, 4, 5, 6, 7]
>>> lfilter = lambda func, xs: functools.reduce(lambda x, y: x + [y] if func(y) else x, xs, [])
>>> lfilter(lambda x: x % 2 == 0, [1,2,3,4,5,6,7,8,9])
[2, 4, 6, 8]
All the examples above, except product (in that regard see another stackoverflow response from Raymond Hettinger), have an existing implementation in Python. Also, all of the functions above are relying on reduce (foldl) and none are taking advantage of foldr.
Final Example
To avoid ending on a dried note and to justify the functional workout executed in the sections above, here is a simple scenario that may demonstrate a decent usage of foldl and foldr in Python. Peter Drake presents this construct in his Lambdas and folds Youtube video. Imagine that, given a list, we need to identify the last and/or the first element that satisfies a certain predicate. This could be written as follows:
import functools
def foldl(func, acc, xs):
return functools.reduce(func, xs, acc)
def flip(func):
@functools.wraps(func)
def newfunc(x, y):
return func(y, x)
return newfunc
def foldr(func, acc, xs):
return functools.reduce(flip(func), reversed(xs), acc)
def first(func, acc, xs):
return foldr(lambda x, y: x if func(x) else y, acc, xs)
def last(func, acc, xs):
return foldl(lambda x, y: y if func(y) else x, acc, xs)
print(last(lambda x: x<8, 99, [1,2,3,4,5,6,7,8,9])) # => 7
print(first(lambda x: x>3, 99, [1,2,3,4,5,6,7,8,9])) # => 4
print(first(lambda x: x>20, 99, [1,2,3,4,5,6,7,8,9])) # => 99
first and last don't require any loop or explicit recursion. first uses foldr taking advantage of the right folding whereas last relies on foldl.
Conclusion
In this era of rediscovery of functional programming, there is much more to explore and to apply to languages that are not inherently functional. Arguably, from a pragmatic perspective, there may be little we need that is not already provided in the current versions of Python and that would require some sophisticated folding mechanisms. Further more, other higher-order functions flagships along with fold, like map and filter, can be expressed in Python with elegant list comprehensions and generator expressions, but this should be the subject of a different article.
Resources
- Python
- Haskell
- Haskell REPL
- Introduction to Functional Programming using Haskell
- Thinking Functionally with Haskell
- Fold
- Richard Bird
- Philip Wadler
- Alex Martelli
- Raymond Hettinger
Release Notes
- 08/28/2016: Initial publication of this article.
Legal
The source code accompanying this article is released under the MIT License.
Credits
- Fold Left image By Cale Gibbard - English Wikipedia, created by Cale Gibbard in Inkscape who released it into public domain, Public Domain
- Fold Right image By Cale Gibbard - Taken from English Wikipedia, created by Cale Gibbard in Inkscape who released it into public domain, Public Domain